If you are teaching bearings online you will need a clockwise 360 degree protractor. This one is held by Wikimedia Commons so you can download and use it in accordance with the licence given.
I am having a bit of a craze on Factors at the moment. I searched the web for “Fun with Factors” and came across this brilliant and very simple game on the NRICH website.**
There’s a neat online version or you can play a pen and paper version. I am likely to spend a while playing the online version today! What’s the longest chain you can make? I managed 18.
If you are aiming for a depth of understanding of Factors, then play as many games as possible – this is a really simple game for 2+ players that just needs 2 dice and a CASIO scientific calculator.
If you know another great factorising game, put it in the comments below!
**The game works brilliantly on a laptop but not so strong on an android phone.
I had an email from B. this morning. He is helping his granddaughter with her Maths and things have changed a bit since he was at school! (I can relate to that too). He said:
“Can the factors of a number (360) be found by using a casio calculator fx -85GTX? Ans: 1, 360, 2, 180, 3, 120 etc”
The answer is yes.
Tip for clever clogs… if you “end” your table with the square root of the number (in this case, √360), you won’t get any repeats, and you can be confident you have found all possible factors!
Ratio Grids Activity …………. Answers …. More Help
Ratio Questions ………………. Answers …. More Help
Percentage Problems ……………………. Video answers
100 Percent ……………………… Answers …. More Help
You can find the Exterior angle in a regular polygon by using Ratio Grids if you want to.
If you are not already confident using RATIO GRIDS then watch this video first!
What is 35% of £14?
What is 15% of £85?
My savings target is £5500. I have saved £2640. What percentage have I saved?
Jo scored 65% in a test. She scored 26 marks. What was the test marked out of?
A tree was 15m tall in January. Now it is 18m tall. What is the percentage increase in height?
Another tree has grown 15% since January. It is now 46m high. What was its height in January?
Now try some problems yourself:
Check out the Introduction to Ratio Grids if you are not already an expert!
When you are asked to do a currency conversion, you will usually be given an exchange rate first, as in this question:
Draw a simple Ratio Grid and give headings of £ and €. Put the numbers 1 and 1.18 in the correct columns. Then, the final number from the question, £350, goes in the £ column under the 1. Putting the numbers into their correct places is easy if you have headings! Put a ring around the empty space – that is where your answer will go.
In this grid, the 2 multiplying numbers are the “1.18” and the “350”, and you will divide by 1. So the sum will be 1.18×350÷1.
The answer is 413, and it is clearly in the Euros column, so give your answer as €413.
It’s easy if you get the headings right!
If you want lots of practice, Mr Corbett has a great set of currency conversion questions.
For lots of simple questions click here and the answers are here
Exam-style questions are here** and the answers are here. (Mr Corbett doesn’t use Ratio Grids so his methods won’t look the same, but the answers are all the same, obviously!)
** Some of these questions are really challening – they may require 2 ratio grids, so think carefully! If an exchange rate changes, you will need a new grid for the new rate.
If you don’t yet know how to work out the 4th number in a ratio grid, watch this video first!
The videos on this page use the worksheet “Ratio Problems” which you can download:
Answers
Ratio Grids can be used whenever you have a problem that starts with 3 numbers, and you have to times and divide. They are a clear way of laying out your working, and knowing which order to do the calculation.
You will need a calculator to do the practice questions, but first, here is a video:
Your comments are very welcome – please use the box below.
Now you can use Ratio Grids to solve a Maths Problems, here are some types of problem you can try:
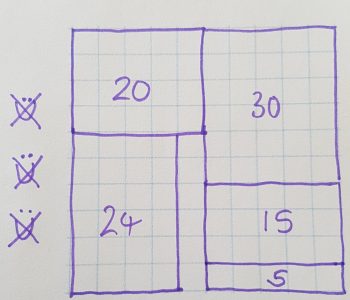
If you know a student has rather problematic times tables, and/or is not confident working with areas, then this game will help you to assess what the scope and nature of the problem is. Please read the notes about what to say before each round – if you “teach” all the strategies in advance, the game won’t be fun any more!
3 or 4 sheets of printed hundred squares“Here is your new game board – by the way how many small squares is it made up of?”
Most will count the first row with their finger. If they do it without a finger, they may get to 9 or 11. If that does happen, I suggest saying “oops, I think you need to check that”. Wait until they have “10”.
Do they then count the number of rows next? Or count each square in the next row? Or count down the rows saying 10, 20, 30?
Wait until they have 100.
“So the maximum score for you will be 100.”
This step will tell you what strategy your pupil is comfortable using to find areas.
“Shall I start so you know what to do when it’s your turn?”. (This avoids the need for too many words!).
“Throw the dice, and use the 2 numbers to draw a rectangle. I’ve thrown 4 and 5. 4 and a 5 give you a 4×5 rectangle. Your score would be 20 for that, because it has 20 squares inside. That’s the area of the rectangle.” (You’ve explained it without putting them on a back foot by asking them for any of the information. You are only telling them how to play, not how to win.
Take turns to throw 2 dice and draw a rectangle. If a dice goes on the floor, say “Oh, it doesn’t count if it goes on the floor. You’ll have to roll it again”. This keeps the game calm!
How do they find the areas? Always count? Count correctly? Make mistakes with counting? Sometimes say “5,10,15,20”, sometimes say “5 5s are 25”?
This observation is *key* to what they may learn today. Choose the lowest level of skill (if they can’t confidently count, don’t worry about tables!!).
You should model at and just above their secure level of skill.
- They count badly? You use dots.
- They count well in ones? You count in 2s and 3s
- They know some of the tables facts? You use others
- They look up some facts on their chart? You look up all of them to reinforce this is a good strategy.
Once one of you has “blocked” most of the board, you will both need to draw 3 lives and each time you have a dice throw you cannot draw, you will lose a life. Once you are dead, the other player continues until they are dead.
Once both are dead, total up the scores you each have.
As they add their score, notice how they do it? Are they correct? Do they want you to do it? Can they add the numbers silently in their head? Do they want to jot the sum? do they want a calculator?
If they struggle and are unhappy, be helpful. Addition can be worked on with a different game on another occasion.
Did they sensibly squeeze the rectangles onto the board? Or spread them out and waste space? Are they ready for a “nudge” on strategy, and start being more efficient? Or are they still overwhelmed by the skills needed for this game?
If you decide to nudge, give specific advice like “why not draw this one in the corner here, to leave room for big ones later?”. This is simpler than trying to explain in an abstract way.
If you decide not to nudge, then aim to lose by spreading your rectangles out. if they make a comment, you can say “I’m trying a different approach this time to see what happens”.
Aim for an understanding of some strategies work better than others rather than one being more “right” or “clever” than another.
The winner of each round gets a counter. Play best of 5 games.
If this whole game is too easy, then draw triangles instead. These may be all right angled or for very advanced version, allow scalene triangles. Discuss areas in either case. Use a ruler!
Bellropespider 
