Click an image below to see it full screen then print it out.
Free Printable Axes for drawing graphs
Leave a reply
Author Archives: Rosalind Martin
Shape Factory
Puzzle to interest students in the rather dry subject of the names of shapes. Part A free-form, Part B, aiming for specific shapes.
Ratio Grids Topic Overview
I invented “Ratio Grids” to help students who struggle with Proportional Reasoning. The philosophy includes:
- All proportional reasoning sums are essentially the same – times 2 numbers and divide by a third. If one of the numbers is one, then it’s just a multiply or a divide.
- Students who get used to working a problem “forwards” often struggle to work backwards, but mathematically there is no difference!
- Skills gained working with ratios can be applied to shopping, percentages, similar shapes, stratified sampling, speed, density, and other “per” problems, Direct and Inverse proportion, currency conversions, unit conversions and the Sine Rule, without learning shed loads of new stuff.
- Students often get in a muddle because they do sums and lose hold of the units of numbers so although they get a correct answer they don’t realise what it means! Ratio hold the units of numbers as well as the numbers themselves.
- Students sometimes try to mix different units inappropriately in their working. With ratio grids this is much less likely.
- Start at the beginning with the Introduction to Ratio Grids
Fraction of a Number Free Printable Maths Dominoes
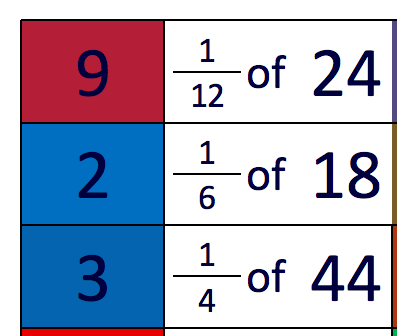
These work best if they are printed onto card, laminated, then cut up. To play, shuffle them, place them face up, and pick an easy question. Find the answer to that question, chain that card on, repeat…
Game – Prime Number Recognition
You will need:
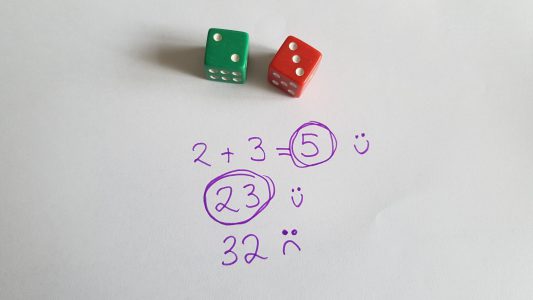
2 dice and a pen and paper.
Take in turns to:
- Throw the dice
- From the dice, construct 2 or perhaps 3 numbers. For example, if you throw a two and a three, you can make 5, 23 and 32 (3+2=5, two followed by three is 23 and three followed by two is 32)
- Score one point for each prime number you have made (so this example scores one for the 5 and one for the 23, scoring two points in total).
- If you need to use a calculator, then a Casio fx-83GT PLUS can tell you whether a number is prime. This is *not* cheating – students will soon start to recognise the primes they need, rather than having to check using the calculator!
The Winner Is:
The person who has the most points.
Things to discuss:
- Why are two even numbers always such bad news? (even+even=even and the only even prime number is two)
- Is it possible to score three points with one throw?
- If there is a six in your throw, what happens?
This sample space diagram may help:
|
Sample Space Diagram for 2 Dice |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1 |
(1,1) |
(2,1) |
(3,1) |
(4,1) |
(5,1) |
(6,1) |
|
2 |
(1,2) |
(2,2) |
(3,2) |
(4,2) |
(5,2) |
(6,2) |
|
3 |
(1,3) |
(2,3) |
(3,3) |
(4,3) |
(5,3) |
(6,3) |
|
4 |
(1,4) |
(2,4) |
(3,4) |
(4,4) |
(5,4) |
(6,4) |
|
5 |
(1,5) |
(2,5) |
(3,5) |
(4,5) |
(5,5) |
(6,5) |
|
6 |
(1,6) |
(2,6) |
(3,6) |
(4,6) |
(5,6) |
(6,6) |
How to Factorise a Number (Or Check that is Prime) using a CASIO fx-83GT PLUS calculator
On the CASIO fx-83gt PLUS factorising is done like this:
- Entering the number,
- press equals,
- SHIFT and ., ,,, (this has “FACT” written above it in yellow).
- The Prime Factor Form is displayed as the answer.
- If the number is Prime, then the number itself is displayed.
This is a natural way to introduce what indices mean, because the CASIO gives the answers in index form eg 34 rather than 3x3x3x3
How to generate a random number under 1000 on a CASIO fx-83GT PLUS
CASIO calculators have a very useful function of generating random numbers. Left to their own devices, they will choose a number between 0 and 1, with 3 decimal places. If you want a WHOLE NUMBER then you need to type 1000 Shift Ran# then press the equals button = . Here is a quick (silent) film showing you how to do it.
Dyscalculia and Dyslexia
A word about Dyscalculia and Dyslexia
According to Brian Butterworth, Dyscalculia is a severe lack of awareness of number, coupled with great difficulty in performing arithmetic tasks. Research and Diagnosis in the UK is still at a relatively early stage, I can recommend the writing of Jan Poustie (herself a sufferer) as an excellent start for the reader wishing to be able to “see the world through Dyscalculic eyes”, and for practical suggestions of how to cope. ** the best book – Mathematical Solutions Part B is available from the author (see comment below)
Butterworth suggests that about 4% of the population may “have dyscalculia”. Looking at the bigger picture, it is clear to anyone working with maths education that a far larger proportion of the population struggle with aspects of Maths, and do not thrive on the traditional approach.
I prefer to see “number blindness” as a spectrum, on which some people are extremely fluent and comfortable with number, to the extent that they seem truly gifted, others struggle painfully, and the majority are somewhere in between, often feeling that they are worse than average, even if they in fact are right in the middle. I start work with every student assuming that they are “number-blind” until I see evidence to the contrary. This helps me to remember that, compared with a Maths teacher, most people are relatively number-blind. Unless you immerse yourself in number as much as a teacher probably has, you may not recognise high powers of two, multiples of large primes like 17, etc etc.
Many Dyslexics struggle with Maths, perhaps because of the extremely complicated processes required to carry out the high-end of arithmetic operations, such as pen and paper division. I am privileged to have worked with a handful of severely dyslexic students, who were very articulate about their learning styles and helped me to experiment with how to express Mathematical reasoning in a way that they could make sense of. Poustie indicates that individuals may well be experiencing some degree of Dyslexia and Dyscalculia, together.
Labels such as Dyslexia and Dyscalculia are only helpful if you have some strategies for coping with them, and I tend to focus on the learner, the Maths, and the strategies, and not worry too much about labels.
I welcome feedback, please use the reply box.
A very elegant piece of algebra
I set this problem today, during a lesson in which we had been looking at simultaneous equations with 2 unknowns:
A + B = 92
A + c = 57
B + C = 59
M came up with this answer:
POSTSCRIPT –
M then set me this problem:
A-B = 25
B+C = 151
A+C = 176
which turned out to have an unexpected twist in it….. Have fun!
Subtraction Confusion – a very simple solution
Do any of your students get in a mess with “double borrowing”? There’s a very simple solution which builds on their existing knowledge of subtraction with borrowing….
Easy subtraction – one “layer” of borrowing
- Much harder subtraction – the borrowing cascades from left to right and is very likely to go wrong.
There is a very simple solution to this, encourage the student to look at the number differently. Borrow ONCE from the “200” on the top, which becomes 199.
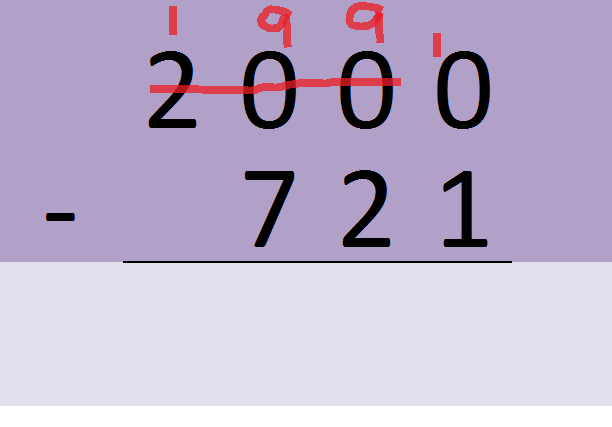
Borrow ONCE from the “200” in the top number – now this sum is ready to do, and there’s far less that can go wrong.
Try it on a student near you, and use the reply box to tell readers what happened next!
Bellropespider 